Modern control: Solutions & state transition matrices
The state equation for a linear time-invariant system:
$$ x’(t) = A x(t) + B u(t) $$
Can be solved for $x(t)$. We collect all terms in $x$:
$$ x’(t) - A x(t) = B u(t) $$
Multiply equation by $e^{-At}$
$$ x’(t) e^{-At} - A x(t) e^{-At} = B u(t) e^{-At} $$
Using product rule $d(f;g) = f;dg + g;df$, where:
$$ \begin{align*} df = - A e^{-At} \rightarrow & f = e^{-At} \\ dg = x'(t) \rightarrow & g = x(t) \\ \\ \therefore x'(t) e^{-At} - A x(t) e^{-At} &= d (e^{-At} x(t)) \end{align*} $$ To give:
Modern control: State space equations
In modern control approaches, systems are analyzed in time domain as a set of differential equations. Higher order differential equations are decomposed into sets of first order equations of state variables that represent the system internally. This produces three sets of variables:
Input variables are stimuli given to the system. Denoted by $u$. Output variables are the result of the current system state and inputs. Denoted by $y$. State variables represent the internal state of a system which may be obscured in the output variables.
Classical control: Transfer functions
A transfer function relates the output of a system to its input when it is represented in the Laplace domain. An assumption is made that initial steady-state response is 0. If $Y(s)$ is the output of a system, $X(s)$ is the input, then the transfer function is:
$$ H(s) = \frac{Y(s)}{X(s)} $$
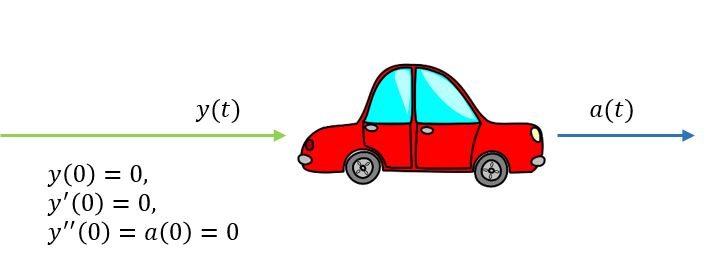
Example - A Car A car as a system: The input is the acceleration. The output is the total distance travelled.
